
Offbeat metronomes reveal chimera state
When you place a series of metronomes on a swing, they start to synchronise themselves automatically. Now a clever experiment shows that the metronomes can also divide themselves into groups where only half of them swing to the beat.
The show is over and the audience is applauding like mad. After only a few seconds, everyone is clapping to the same beat while the actors take a bow.
We humans are not the only ones capable of spontaneously finding the beat. Nature has numerous examples of this phenomenon.
The synchronisation of coupled oscillators is a striking form of self-organisation that nature employs to orchestrate essential processes of life, such as the beating of the heart. Our hearts would not function if the many heart cells were unable to find the beat. And if you go to the tropics, you may be fortunate enough to spot swarms of fireflies that flash to the same beat.
If you start up a series of metronomes on a steady surface, they will obviously not suddenly start beating like one. They will, however, if they are placed on a swing or a plate that can move along with the metronomes.
“The metronomes are lulled into a synchronised rhythm,” says Erik Andreas Martens, a postdoc fellow at DTU Aqua, the National Institute of Aquatic Resources at the Technical University of Denmark.
Martens is the lead author of a new study, published in the journal PNAS, which reveals an entirely new dimension of the synchronisation phenomenon.
Chimera states – in between synchrony and disorder
It was long thought that synchrony and disorder were mutually exclusive steady states for a network of identical metronomes, or oscillators in general. However, many theoretical studies have revealed the possibility of ‘chimera states’ in which the symmetry of the metronome population is broken into a synchronous part and an asynchronous part.
Mathematicians have known this for a decade, but it isn’t until now that the phenomenon has been demonstrated in an experiment. This took place at the Max Planck Institute for Dynamics and Self-Organization in Göttingen, Germany.
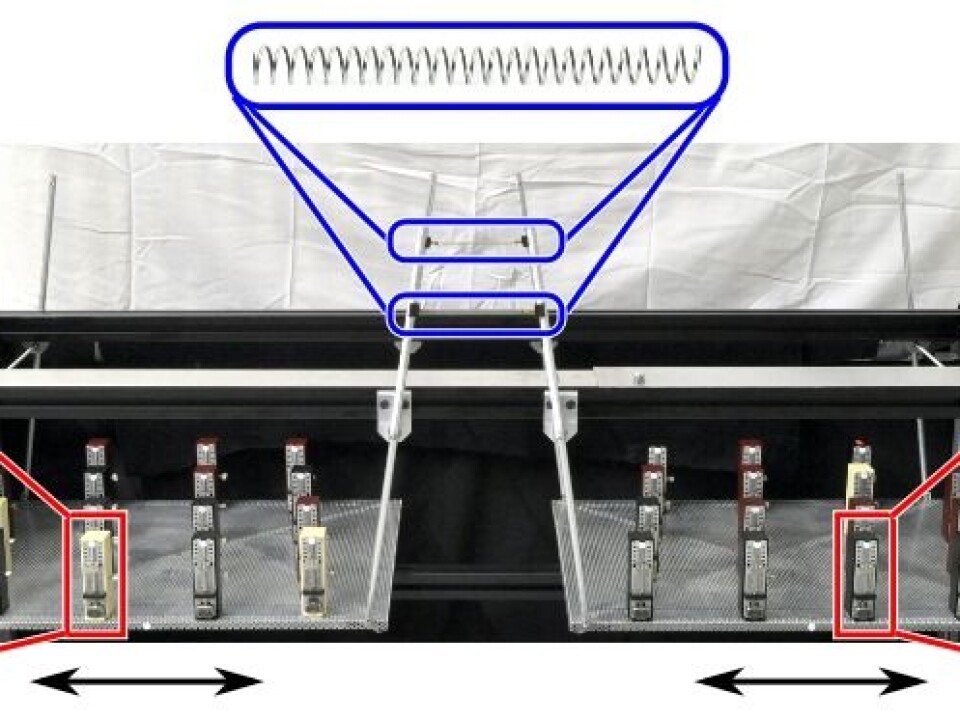
“We placed metronomes on two swings that are connected with springs. This brings about the chimera state,” says Martens.
Thirty metronomes trying to organise themselves
On one of the swings, all 15 metronomes were quick to find the beat, but on the other swing the metronomes never managed to synchronise themselves.
Identical units coupled in a hierarchical network have never before been observed to organise themselves into an orderly and a disorderly state in this way.
So what is the value of these findings?
”We only used masses, springs and pendulums – i.e. very elementary building blocks. And they have direct analogues in electronic and chemical networks. So it seems very likely that other systems may also exhibit these chimera states. Chimeras may either be states that jeopardise synchrony where it is wanted, or they may be a feature in technological applications.”
Mathematics enters the real world
The researcher mentions alternating current in the grid as an example of the importance of synchronisation. A sudden glitch in the grid may cause the alternating currents to start beating out of phase in different lines, thus making the grid nonsynchronous. This may cause power outages, so it is important to design electricity systems so that they are resistant to chimera states.
”One could also imagine technological applications with micromechanical oscillators where only half of them will swing to the beat,” says Martens.
“We’re still not entirely sure what our research can lead to. Only the future can tell. But now we have achieved a breakthrough in connecting the extremely abstract mathematical models to the real world with our experiment.”
----------------------
Read the Danish version of this article at videnskab.dk
Translated by: Dann Vinther




